

As we mentioned in the previous chapter, many functions are locally linear, so if we restrict the domain the function will appear linear. Thus we often start with linear models when trying to understand a situation. In this section we look at the concepts of supply and demand and market equilibrium. For our examples in this section we will assume that the functions are linear in the range we care about.
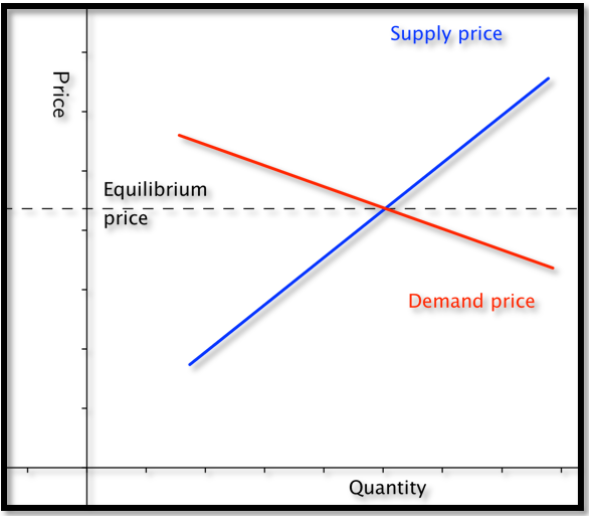
Figure \(2.1.2.\) Video presentation of this example
Suppose \(q\) denotes quantity, and the supply price for widgets is given by
We are also told the demand price is given by
\[ Demand \ price=\$18-\frac\text <.>\nonumber \]
Find the equilibrium price and quantity.
Solution
We have started with an example that we can do by basic algebra without any technology. Subtracting the two equations, we see that
Some straightforward algebra shows that the equilibrium quantity is 400. Substituting back into either equation gives an equilibrium price of $10.
While we can do this example by hand, we also want to use it to set up a solution with Excel, since we may want help on problems where the numbers are not as nice. Our plan is to use Goal Seek to find the intersection. We need a cell where we can solve the problem by forcing the cell to have a value of zero.


When cell D2 is zero, the supply price will be the same as the demand price. We now invoke Goal Seek.

As expected, it finds equilibrium when \(q=400\text<.>\)
We need to do a bit more work when we are simply given data points and need to find the supply and demand curves.
Figure \(2.1.4.\) Video presentation of this example
My market data indicates customers will buy 700 gizmos if they are priced at $13 each. If the price rises to $15, they will only buy 500. If the price is $12 a unit, the producers will make 400 gizmos. If the price rises to $13, they will produce 600 gizmos. Assume that the supply and demand curves are linear for between 300 and 1000 gizmos. Find the equilibrium point for the gizmo market.
SolutionWe start by making a chart for the values given. We add a scatterplot so that we can see the values.
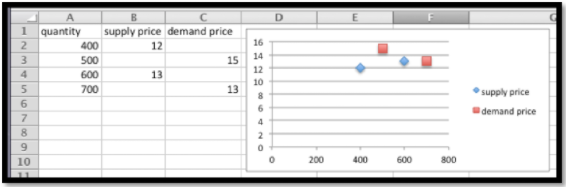
Next we add linear trendlines for both the supply and demand. We select the option to show the equations.

The projected equations are:
We set up columns for the projected supply and demand curves. We also add a column for the difference so that we can use Goal seek to find the equilibrium point.

It is then straightforward to see that the equilibrium quantity is 666.67 and the equilibrium price is $13.33.

There is one more detail worth noting from this last example. Depending on the units used, the slope can be very close to zero. If we are selling tens of millions of units for a price under a dollar, the change in price of a penny may correspond to a change in quantity of several thousand. Make sure to include enough digits for your equation to be meaningful.
Figure \(2.1.6.\) Video presentation of this example
We have obtained the following data for sales of gizmos in our location.
| quantity | 653 | 762 | 847 | 943 | 1050 | 1130 | 1260 |
| Supply price | 5.52 | 6.20 | 6.85 | 7.48 | |||
| Demand price | 6.68 | 6.50 | 6.38 | 6.31 |
Assume the supply and demand curves are linear for quantities between 600 and 1300. Find the best fitting lines for the supply and demand functions. Find the equilibrium point. Make a chart listing how many we can sell for $6.40 and $6.60. Remember that sales will be the minimum of the supply and the demand.
Solution
We start by putting the data into a spreadsheet and finding the best fitting lines. We select the option to show the equations in the chart.


The supply and demand functions are:
\begin \text\amp =.0032*\text+3.44\\ demand\ price\amp =-0.0010*quantity+7.46\text <.>\end
We add columns for the projected supply and demand prices, using the equations obtained from the best fitting lines. We also add a column, and compute the difference of the supply and demand functions. We can now use goal seek to solve the problem.

We now use Goal Seek to find the equilibrium point.
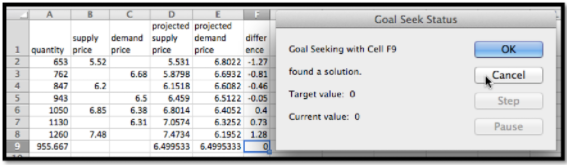
At equilibrium we sell 956 gizmos at $6.50. To find sales at $6.40 and $6.60, we use Goal Seek to get those values at both supply and demand prices.

We see that we can sell 1055 gizmos at $6.40, but can only obtain 925. Thus our sales at $6.40 will be 925. At $6.60 we can obtain 987 gizmos, but can only sell 855. Thus our sales at $6.60 will be 855. We can eliminate a step in this process if we recall that below equilibrium price the constraint is supply, while above equilibrium price the constraint will be demand.
Given \(supply\ price=3 quantity+10\) and \(demand\ price=-2 quantity+30\text\) with \(q_0=6\text<.>\)
Answer
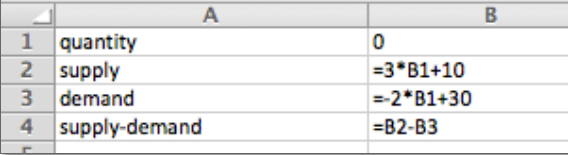

Entries in the cells before quick fill


Table with quantities ranging from 0 to 10
From the table we see that at \(q_0=6\) the supply price is $28 and the demand price is $18.
This page titled 2.1: Market Equilibrium Problems is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Mike May, S.J. & Anneke Bart via source content that was edited to the style and standards of the LibreTexts platform.